Optimal transport group

(MultiFlow) Clément Cancès, Daniel Matthes, Ismael Medina, Bernhard Schmitzer: Continuum of coupled Wasserstein gradient flows, (2024) [preprint] [details]

Motivated by work on local and stratified algorithms for optimal transport we study a system of coupled flows in the space of transport plans that seek to minimize the entropic optimal transport objective. This can be seen as a relaxation of the famous Angenent-Haker-Tannenbaum scheme to entropic transport and we show that this relaxation makes the scheme well-posed and guarantees convergence to the minimizer.

(UnbalancedDomDec) Ismael Medina, The Sang Nguyen, Bernhard Schmitzer: Domain decomposition for entropic unbalanced optimal transport, (2024) [preprint] [details]

While it is rather straight-forward to parallelize domain decomposition for balanced transport, it is more involved for unbalanced transport. In this article we show how this is still possible and yields an efficient method for problems on large grids.

(MultiMaterialHMass) Julius Lohmann, Bernhard Schmitzer, Benedikt Wirth: Formulas for the h-mass on 1-currents with coefficients in Rm, (2024) [preprint] [details]

The multimaterial transport problem is a natural generalization of the Beckmann formulation for the Wasserstein-1 distance, which can also be interpreted as a convex relaxation of certain branched transport problems. Its key feature is a norm-like cost for flows of material vectors, that can be interpreted as matrix valued measures. This cost can be constructed and expressed in several different ways, by duality, by approximation with polyhedral fluxes, or by convex relaxation and an integral formulation. In this article we show that all three constructions coincide, we interpret the primal-dual optimality conditions as generalizations of the Beckmann problem, and we show how the convex relaxation can be interpreted as a homogenization result for microstructures in the flow.

(FlowDomDec) Ismael Medina, Bernhard Schmitzer: Flow updates for domain decomposition of entropic optimal transport, (2024) [preprint] [details]

When running at a single scale on a very fine resolution, conventional domain decomposition for optimal transport can become very slow and fail to resolve curl in the initializing transport plan. We introduce flow updates as a non-local descent direction to remove such curl efficiently.

(SinkhornDistance) Hugo Lavenant, Jonas Luckhardt, Gilles Mordant, Bernhard Schmitzer, Luca Tamanini: The Riemannian geometry of Sinkhorn divergences, (2024) [preprint] [details]

Entropic regularization of optimal transport has several beneficial effects: Efficient numerical methods, better statistical robustness, and it has a wealth of applications in stochastic optimal control. But the metric structure induced by classical optimal transport is lost. De-biased Sinkhorn divergences mitigate this effect to some extent, but they do still not satisfy the triangle inequality. In this article we construct a Riemannian distance by using the Hessian matrix of the Sinkhorn divergence as metric tensor.

(BatchTransfer) Florian Beier, Hancheng Bi, Clément Sarrazin, Bernhard Schmitzer, Gabriele Steidl: Transfer Operators from Batches of Unpaired Points via Entropic Transport Kernels, (2024) [preprint] [code] [details]

This artile builds on EntropicTransfer and infers transfer operators from observations of batches of particles, but without observing their pairwise associations. This is more involved and requires the introduction of a suitable EMML algorithm for inference.

(W2Manifolds) Keaton Hamm, Caroline Moosmüller, Bernhard Schmitzer, Matthew Thorpe: Manifold learning in Wasserstein space, (2023) [preprint] [code] [details]

We introduce a class of `sub-manifolds' in Wasserstein space on which there are quantitative bounds for the linearized optimal transport approximation. At the same time it paves the way for data analysis in Wasserstein space beyond the pointwise local approximation.

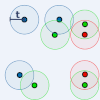(MultiMatch) Julia Naas, Giacomo Nies, Housen Li, Stefan Stoldt, Bernhard Schmitzer, Stefan Jakobs, Axel Munk: MultiMatch: Geometry-Informed Colocalization in Multi-Color Super-Resolution Microscopy, Commun Biol 7:1139 (2024) [published version] [preprint] [details]

We use unbalanced multimarginal optimal transport to model the problem of multichannel particle colocalization analysis. The method comes with a software package and a statistical model for the influence of incomplete labelling efficiencies.

(HamsterLungs) Jakob Reichmann, Clement Sarrazin, Sebastian Schmale, Claudia Blaurock, Anne Balkema-Buschmann, Bernhard Schmitzer, Tim Salditt: Cytoarchitecture of SARS-CoV-2 infected hamster lungs by X-ray phase contrast tomography: imaging workflow and classification for drug testing, Scientific Reports 14:12348 (2024) [published version] [preprint] [details]

This article describes a long pipeline of x-ray phase contrast tomography imaging on hamster lungs, with subsequent analysis of the lung tissue based on the chord length distribution by means of optimal transport, to study the effect of SARS-CoV-2 infections and some subsequent experimental drugs.

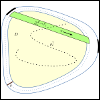(DynPetAnalysis) Marco Mauritz, Bernhard Schmitzer, Benedikt Wirth: A Bayesian model for dynamic mass reconstruction from PET listmode data, SIAM Journal on Mathematical Analysis 56(5), 5840-5880 (2024) [preprint] [details]

This is a follow-up on (DynamicPET-Numerics) to give a rigorous theoretical motivation and analysis for temporal Wasserstein regularization in dynamic PET imaging and for the scatter debiasing step.

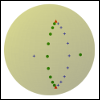(LinOTManifold) Clément Sarrazin, Bernard Schmitzer: Linearized optimal transport on manifolds, SIAM Journal on Mathematical Analysis 56(4), 4970-5016 (2024) [preprint] [code] [details]

We extend the framework of linearized optimal transport in various ways: for base spaces that are manifolds, extension ot the spherical Hellinger--Kantorovich (SHK) distance, more compact and clear expressions for the logarithmic map of HK, and continuity properties of the logarithmic maps (including approximation by discretization).

(EntropicTransfer) Oliver Junge, Daniel Matthes, Bernhard Schmitzer: Entropic transfer operators, Nonlinearity 37(6), 065004 (2024) [published version] [preprint] [code] [details]

Entropic optimal transport is used to regularize a naive discretization of the transfer operator for dynamical systems. We proof that the regularization ensures convergence of the discretization in the limit, on length scales above the entropic blur. This allows for the numerical approximation of spectral analysis of dynamical systems on relatively primitive input data, such as observed discrete noisy trajectories.

(HKDiracBarycenter) Mauro Bonafini, Olga Minevich, Bernhard Schmitzer: Hellinger-Kantorovich barycenter between Dirac measures, ESAIM: Control, Optimisation and Calculus of Variations 29, 19 (2023) [published version] [preprint] [details]

While the barycenter between a collection of Dirac measures is trivial for the Wasserstein-2 metric, it was observed in (HKBarycenter) that in the Hellinger--Kantorovich metric it exhibits a very complex behaviour. In this article we study this structure in more detail, in particular the dependency on the length scale, the relation between empirical and population barycenter, and duality.

(LinOTMS) Jakob Frost, Bernhard Schmitzer, Mareike Toepperwien, Marina Eckermann, Jonas Franz, Christine Stadelmann, Tim Salditt: 3d virtual histology reveals pathological alterations of cerebellar granule cells in multiple sclerosis, Neuroscience 520, 18-38 (2023) [published version] [preprint] [details]

We apply the workflow of (PNAS21), involving linearized optimal transport, to the analysis of multiple sclerosis and its effects on cerebellar granule cells.

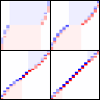(AsymptoticDomDec) Mauro Bonafini, Ismael Medina, Bernhard Schmitzer: Asymptotic analysis of domain decomposition for optimal transport, Numerische Mathematik 153, 451-492 (2023) [published version] [preprint] [code] [details]

The asymptotic behaviour of domain decomposition for optimal transport is studied in the limit of infinitely fine cells. Under suitable conditions this converges to a continuity equation for the coupling on the product space where the momentum field is purely `horizontal' and induced by a limit version of the domain decomposition algorithm. The result suggest that the number of iterations for domain decomposition scales linear with the problem resolution. In combination with coarse-to-fine schemes this could even be reduced to a logarithmic number of iterations and hence supports the numerical findings of (EntropicDomDec).

(BranchedTransportDual) Julius Lohmann, Bernhard Schmitzer, Benedikt Wirth: Duality in branched transport and urban planning, Applied Mathematics & Optimization 86, 45 (2022) [published version] [preprint] [details]

This is a companion work to (BranchedTransportBilevel) in which related results are established via a different proof strategy based on a generalization of the Kantorovich--Rubinstein duality.

(BranchedTransportBilevel) Julius Lohmann, Bernhard Schmitzer, Benedikt Wirth: Formulation of branched transport as geometry optimization, Journal de Mathématiques Pures et Appliquées 163, 739-779 (2022) [published version] [preprint] [details]

The formation of ramified transport networks has been modelled mathematically via the branched transport and urban planning formulation. For the original urban planning formulation an equivalent branched transport formulation has been shown. In this article we extend the equivalence to a more general set of costs on both sides. The proof strategy is based on explicit translation of minimizers between the two problems.

(GameLearning) Mauro Bonafini, Massimo Fornasier, Bernhard Schmitzer: Data-driven entropic spatially inhomogeneous evolutionary games, European Journal of Applied Mathematics 34, 106-159 (2022) [published version] [preprint] [details]

We propose a novel class of models for interacting particles based on spatially inhomogeneous evolutionary games with entropic regularization and then propose an inference functional to learn the agents' payoff function from observations of interactions.

(UnbalancedLOT) Tianji Cai, Junyi Cheng, Bernhard Schmitzer, Matthew Thorpe: The Linearized Hellinger-Kantorovich Distance, SIAM Journal on Imaging Sciences 15(1), 45-83 (2022) [published version] [preprint] [code] [details]

The Wasserstein-2 distance exhibits a weak Riemannian structure, including notions of tangent spaces, logarithmic and exponential maps. This structure has been leveraged successfully for a local linearization scheme which reduces the computational load and provides a linear embedding which is useful for subsequent data analysis tasks. In this article we generalize this approach to the unbalanced Hellinger-Kantorovich distance, which allows the approach to deal with local mass fluctuations in a more refined way.

(PNAS21) Marina Eckermann, Bernhard Schmitzer, Franziska van der Meer, Jonas Franz, Ove Hansen, Christine Stadelmann, Tim Salditt: Three-dimensional virtual histology of the human hippocampus based on phase-contrast computed tomography, PNAS, 118 (48) e2113835118 (2021) [published version] [details]

Phase-contrast X-ray computed tomography is used to generate high-resolution large-volume 3d images of human brain tissue samples, including both Alzheimer’s-diseased patients and a control group. After automated segmentation and feature extraction of certain cell nuclei each sample can be represented as a point cloud on cell feature space. We use the framework of linearized optimal transport to study the population of samples and provide a preliminary identification of the main mode of variation between pathological and control group.

(EntropicDomDec) Mauro Bonafini, Bernhard Schmitzer: Domain decomposition for entropy regularized optimal transport, Numerische Mathematik 149, 819-870 (2021) [published version] [preprint] [code] [details]

We study a domain decomposition algorithm for entropic optimal transport. Unlike the unregularized version it converges to the optimal solution under very mild assumptions. We bound the convergence rate and show that it can be very slow on malicous counter-examples. Conversely, on `nice' geometric problems we find empirically that it converges quickly. A computationally efficient implementation is discussed that compares favourably to a single Sinkhorn algorithm and which can be parallelized efficiently.

(HKBarycenter) Gero Friesecke, Daniel Matthes, Bernhard Schmitzer: Barycenters for the Hellinger-Kantorovich distance over Rd, SIAM Journal on Mathematical Analysis 53 (1), 62-110 (2021) [published version] [preprint] [details]

We study the barycenter of the HK metric. Analogously to the Wasserstein barycenter it can be formulated equivalently as a `coupled-two-marginal' formulation and as a multi-marginal formulation. The HK barycenter between Dirac measures is analyzed in detail. We find that it differs substantially from the Wasserstein barycenter by exhibiting a local `clustering' behaviour.

(DynamicPET-Numerics) Bernhard Schmitzer, Klaus P. Schäfers, Benedikt Wirth: Dynamic Cell Imaging in PET with Optimal Transport Regularization, IEEE Trans Med Imaging 39(5), 1626-1635 (2020) [published version] [preprint] [details]

We apply optimal transport as a temporal regularization for the reconstruction of particle trajectories from low intensity PET data. The regularization is in essence the "energy" of the trajectory in Wasserstein-2 space. This is a numerical proof-of-concept article. A more detailed mathematical analysis will follow.

(GraphTransport) Matthias Erbar, Martin Rumpf, Bernhard Schmitzer, Stefan Simon: Computation of Optimal Transport on Discrete Metric Measure Spaces, Numerische Mathematik 144, 157–200 (2020) [published version] [preprint] [details]

On a discrete metric space the Wasserstein-2 distance does not induce a geodesic space. This implies that there is no displacement interpolation and no notion of a gradient flow. Jan Maas proposed a modified distance by modifying the Benamou--Brenier formula for discrete spaces, based on a Markov kernel. In this article we propose a consistent time-discretization of the optimization problem and a corresponding optimization scheme based on proximal splitting. This allows, for instance, to numerically simulate the heat equation with respect to the Markov kernel as a gradient flow with respect to the new distance.

(SparseScaling) Bernhard Schmitzer: Stabilized Sparse Scaling Algorithms for Entropy Regularized Transport Problems, SIAM Journal on Scientific Computing (SISC) 41(3), A1443-A1481 (2019) [published version] [preprint] [code] [details]

This article builds on (UnbalancedScaling) and discusses some adaptions to the scaling algorithms for entropy regularized transport problems, for more robust and efficient numerical implementation. A log-domain stabilization and epsilon-scaling remedy diverging scaling factors and slow convergence as regularization approaches zero; adaptive truncation of the kernel and a coarse-to-fine scheme similar to (ShortCuts) reduce the requied memory. A new complexity analysis of the Sinkhorn algorithm, based on a comparison to the auction algorithm is developed. Numerical examples demonstrate that the modified algorithm can solve a variety of large transport-type problems with small regularization.

(UnbalancedW1-Dynamic) Bernhard Schmitzer, Benedikt Wirth: Dynamic Models of Wasserstein-1-Type Unbalanced Transport, ESAIM: Control, Optimisation and Calculus of Variations 25, 23 (2019) [published version] [preprint] [details]

This article relates (StaticWFR) with (UnbalancedW1): static and dynamic formulations for unbalanced Wasserstein-1-type transport models are given. In particular it is shown that under suitable assumptions every dynamic model can be rewritten as a (computationally more attractive) static model. Conversely, we study which static models have a dynamic interpretation.

(UnbalancedW1) Bernhard Schmitzer, Benedikt Wirth: A Framework for Wasserstein-1-Type Metrics, Journal of Convex Analysis 26 (2), 353-396 (2019) [published version] [preprint] [details]

In (WFR), (StaticWFR) and (UnbalancedScaling) models for unbalanced transport were studied, where mass can be created or annihilated, with a focus on Wasserstein-2-type transport models. In this article we develop an analogous framework for the Wasserstein-1 metric. The extended models allow to combine the W-1 distance with other local similarity measures. In particular the reformulation as a min-cost flow problem is preserved, which can be solved efficiently. Numerical examples illustrate the robustness of the resulting unbalanced discrepancy measures on noisy data.

(StaticWFR) Lenaic Chizat, Gabriel Peyré, Bernhard Schmitzer, François-Xavier Vialard: Unbalanced Optimal Transport: Dynamic and Kantorovich Formulations, Journal of Functional Analysis 274 (11), 3090-3123 (2018) [published version] [preprint] [details]

This article is a direct continuation of the work in (WFR). We study the geometry of the Wasserstein-Fisher-Rao interpolation and in particular provide a Kantorovich-like static reformulation of the dynamic problem. Since the proof of equivalence between the two formulations hinges only on rather general properties of the functional, we generalize the results to cover a large class of dynamic extensions of optimal transport. This may be an important step in finding efficient numerical solvers to generalizations of dynamic optimal transport.

(UnbalancedScaling) Lenaic Chizat, Gabriel Peyré, Bernhard Schmitzer, François-Xavier Vialard: Scaling Algorithms for Unbalanced Transport Problems, Mathematics of Computation 87, 2563-2609 (2018) [published version] [preprint] [details]

A family of scaling algorithms for entropy regularized transport-type problems is introduced, that generalize the well-known Sinkhorn algorithm for standard optimal transport. Applications involve unbalanced transport problems (in a formulation given by [Liero, Mielke, Savaré], related to the formulation given in (StaticWFR)), JKO-type gradient flow schemes and (unbalanced) barycenters. The article provides an analysis of the algorithms in a continuous setting, comments on practical implementation for discretized problems and several numerical examples.

(WFR) Lenaic Chizat, Gabriel Peyré, Bernhard Schmitzer, François-Xavier Vialard: An Interpolating Distance between Optimal Transport and Fisher-Rao Metrics, Foundations of Computational Mathematics 18: 1-44 (2018) [published version] [preprint] [details]

Based on the dynamic formulation of optimal transport due to Benamou and Brenier, this paper introduces an interpolation between the classical L2 optrimal transport distance and the Fisher-Rao metric. For this a source term is added to the continuity equation which allows for generation and removal of mass. We analyze the corresponding optimization problem in the context of convex optimization and study in particular geodesics between Dirac measures. Finally, a numerical scheme is presented and some examples illustrate the usefulness of this particular growth term for image interpolation.

(EntropicOT) Guillaume Carlier, Vincent Duval, Gabriel Peyré, Bernhard Schmitzer: Convergence of Entropic Schemes for Optimal Transport and Gradient Flows, SIAM Journal on Mathematical Analysis 49 (2), 1385-1418 (2017) [published version] [preprint] [details]

Entropy regularization has recently been re-introduced as an efficient numerical method for approximately solving problems involving optimal transport. In this article we investigate the convergence to the unregularized problem. We show that the regularized transport functional Gamma-converges to the standard functional in the limit of vanishing regularization. Analogously, we show that the implicit time-discrete Wasserstein gradient flow scheme for non-linear diffusion, with a regularized transport functional, converges to the same PDE-limit as the unregularized scheme, if regularization decreases sufficiently fast with decreasing time-step size.

(ImageAssignment) Freddie Åström, Stefania Petra, Bernhard Schmitzer, Christoph Schnörr: Image Labeling by Assignment, Journal of Mathematical Imaging and Vision 58(2), 211-238 (2017) [published version] [preprint] [details]

This article introduces a non-convex framework for the image labelling problem. A (fuzzy) labelling of an image pixel is represented by a discrete probability distribution. Starting from the completely undecided fuzzy labelling, the final image labelling is obtained by following a Fisher-Rao gradient flow, where the energy is determined by the discrepancy of a pixel labelling from its local expectation (determined by the observed data) and the labels of the neighbouring pixels. The flexible mathematical formulation allows for application to rather different problems.

(ShortCuts) Bernhard Schmitzer: A Sparse Multi-Scale Algorithm for Dense Optimal Transport, Journal of Mathematical Imaging and Vision 56 (2): 238-259 (2016) [published version] [preprint] [code] [details]

This is an extension of (SSVM'15). Analogous to continuous optimal transport, a framework for locally verifying global optimality of a given coupling is developed, leveraging the geometric structure of the underlying cost function. This leads to a sparse multi-scale algorithm for large dense problems. Various cost functions (including the squared Euclidean distance and the squared geodesic distance on the sphere) and noisy variants thereof are detailed explicitly. Numerical experiments demonstrate a substantial decrease in memory requirements and a speed-up of around two orders of magnitude compared to the naive dense approach.

(WassersteinModes) Bernhard Schmitzer, Christoph Schnörr: Globally Optimal Joint Image Segmentation and Shape Matching based on Wasserstein Modes, Journal of Mathematical Imaging and Vision 52 (3): 436-458 (2015) [published version] [preprint] [details]

This is a more detailed analysis of the ideas developed in (EMMCVPR'13) for object segmentation and matching with a prototype template. Based on the relation developed in (ShapeMeasures) we use contour-based statistical learning methods to obtain a set of non-isometric Wasserstein modes to describe typical deformations of the template. Locally adaptive appearance models are studied and different optimization schemes are discussed in detail.

(ShapePriorGW) Bernhard Schmitzer, Christoph Schnörr: Modelling convex shape priors and matching based on the Gromov-Wasserstein distance, Journal of Mathematical Imaging and Vision 46 (1): 143-159 (2012) [pdf] [published version] [details]

Representing shapes by so called metric measure-spaces (mm-spaces) and comparing them by the Gromov-Wasserstein distance has proven to be an elegant way to overcome issues like reparametrization ambiguity and to abstract from transformations that a shape can undergo while still remaining basically the same shape. However the involved optimization problems are highly non-convex. In this paper we present a series of suitable approximations to the Gromov-Wasserstein functional and arrive at a modified linear optimal transport problem for finding a registration between a given shape template and its most probable instance within the query image. To our knowledge this is the first time that a shape prior functional is presented, that is both convex and invariant under various geometric transformations.

(SPOT) Yikun Bai, Bernard Schmitzer, Mathew Thorpe, Soheil Kolouri: Sliced Optimal Partial Transport, CVPR 2023 (2023) [published version] [preprint] [details]

We give an adapted version of the Hungarian method to efficiently solve one-dimensional partial OT problems. This is then used for applying partial sliced OT to geometric problems such as noisy shape registration.

(SSVM'17) Jan Henrik Fitschen, Friederike Laus, Bernhard Schmitzer: Optimal Transport for Manifold-Valued Images, Proceedings of the 6th International Conference on Scale Space and Variational Methods in Computer Vision (2017) [pdf] [published version] [details]

An extension of optimal transport to non-scalar signals such as color images is constructed by lifting the original signals to non-negative measures on a higher dimensional space. It is natural to use unbalanced transport in this setting. Numerical optimization is handled with the algorithms developed in (UnbalancedScaling) and (SparseScaling). We give examples for interpolation between color images in different color spaces as well as a simple classification example on the MNIST dataset.

(SSVM'15) Bernhard Schmitzer: A sparse algorithm for dense optimal transport, Proceedings of the 5th International Conference on Scale Space and Variational Methods in Computer Vision (2015) [pdf] [published version] [details]

This is a continuation of the work started in (SSVM'13) to develop sparse algorithms for solving dense discrete optimal transport problems. In (SSVM'13) the structure of the cost function is only exploited implicitly, hoping that only few hierarchical consistency checks are necessary. Here on the other hand, the structure is explicitly used, resulting in `truely' sparse algorithms. Compared to (SSVM'13) this approach is less flexible in terms of cost functions, but more flexible in terms of which algorithms one can accelerate, resulting in lower running-times.

(EMMCVPR'13) Bernhard Schmitzer, Christoph Schnörr: Object Segmentation by Shape Matching with Wasserstein Modes, Proceedings of the 9th International Conference on Energy Minimization Methods in Computer Vision and Pattern Recognition (2013) [pdf] [published version] [details]

In (ShapePriorGW) we used optimal transport to compute an assignment between a reference template and its most likely counterpart in a query image. Geometric invariance was obtained by a particular cost function, computed in a pre-processing step, based on an approximation to the Gromov-Wasserstein distance. In this paper we explicitly optimize over the embeddings of the reference template into the image domain. Standard squared Euclidean distance is used as cost function, making the rich Monge theory of optimal transport applicable. Using the manifold structure of measures, equipped with optimal transport, we can describe isometries and non-isometric deformations in a unified way. Global optimality of the non-convex model is obtained via a branch and bound scheme, based on locally adaptive convex relaxations.

(SSVM'13) Bernhard Schmitzer, Christoph Schnörr: A Hierarchical Approach to Optimal Transport, Proceedings of the 4th International Conference on Scale Space and Variational Methods in Computer Vision (2013) [pdf] [published version] [details]

The linear assignment and optimal transport problem are not only important tools in our own line of research but pervade models in computer vision and machine learning. Practical problems often come with a cost function which is far from arbitrary, but in fact rather regular. Unfortunately efficient solvers that exploit the structure of cost functions are rare (except for the squared Euclidean distance, of course). In this paper we discuss an extension of the famous auction algorithm, to turn large, dense optimal transport problems into sparse subproblems, guaranteeing global optimality by a hierarchical consistency check. We observe a significant gain in performance on a wide range of test problems (in particular beyond squared Euclidean distance in real vector spaces).

(SSVM'11) Bernhard Schmitzer, Christoph Schnörr: Weakly Convex Coupling Continuous Cuts and Shape Priors, Proceedings of the 3rd International Conference on Scale Space and Variational Methods in Computer Vision (2011) [pdf] [published version] [details]

In this paper we demonstrate that enhancing binary foreground/background segmentation by the aid of a shape prior is in principle possible in a convex variational framework. Two simple shape models, both represented by Markov random fields (MRF), are considered. The segmentation problem is formulated in a convex variational way via the famous continuous cuts functional. A convex shape prior functional is obtained from the shape model through the local polytope relaxation of the underlying MRFs. The two components are coupled by a quadratic term yielding a convex overall functional which we optimize globally with a recent algorithm from convex optimization.

(VimentinCurvature) Anna Blob, David Ventzke, Giacomo Nies, Jan Niklas Dühmert, Bernhard Schmitzer, Axel Munk, Laura Schaedel, Sarah Köster: Vimentin intermediate filaments structure and mechanically support microtubules in cells, (2023) [preprint] [details]

This is a long and detailed experimental study of the relation between vimentin and the curvature and orientation of the microtubule network. Our group provided a part of the analysis: comparing and analyzing one-dimensional distributions over curvature with the (linearized) optimal transport framework. Unfortunately, there were some other confounding factors in the data that compromised the study of the relation between vimentin and the microtubule network and therefore this preprint will not be published in a peer-reviewed journal. However this work will be continued both form a biophysical and methodological perspective.

(SemiDiscreteUnbalanced) David P. Bourne, Bernhard Schmitzer, Benedikt Wirth: Semi-discrete unbalanced optimal transport and quantization, (2018) [preprint] [details]

We combine the concepts of semi-discrete transport with unbalanced transport and generalize the `tessellation' formulations for semi-discrete classical optimal transport. The intrinsic length scale of unbalanced transport leads to interesting effects. Finally, we study the unbalanced quantization problem and its asymptotic behaviour in the limit of infinitely many points.

(ShapeMeasures) Bernhard Schmitzer, Christoph Schnörr: Contour Manifolds and Optimal Transport, (2013) [preprint] [details]

In (EMMCVPR'13) we represented shapes by measures with indicator functions as densities, using the pseudo-Riemannian structure of the Wasserstein space of measures for modelling isometries and statistical variations. In this paper we provide a mathematical study of the shape measure representation and its relation to the contour description. It turns out that both representations are equivalent in the sense that the two corresponding manifolds are diffeomorphic. We claim that this can be used to combine the usefulness of the natural linear structures on indicator functions as well as on tangent-space approximations to contour manifolds for image processing tasks.

Olga Minevich: Adaptive numerical methods for optimal and branched transport problems, Universität Göttingen (2023) [published version]

Bernhard Schmitzer: Isometry Invariant Shape Priors for Variational Image Segmentation, Universität Heidelberg (2014) [published version]

Dionigi M. T. Benincasa, Fay Dowker, Bernhard Schmitzer: The Random Discrete Action for 2-Dimensional Spacetime, Class. Quantum Grav. 28 105018 (2011) [published version] [preprint]

Bernhard Schmitzer, Wolfgang Kinzel, Ido Kanter: Pulses of chaos synchronization in coupled map chains with delayed transmission, Phys. Rev. E 80, 047203 (2009) [published version]